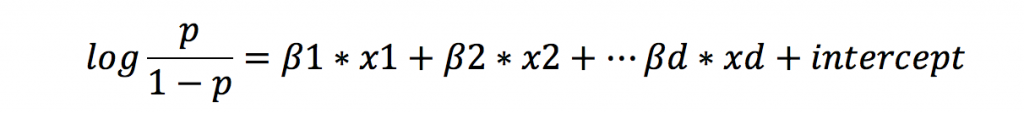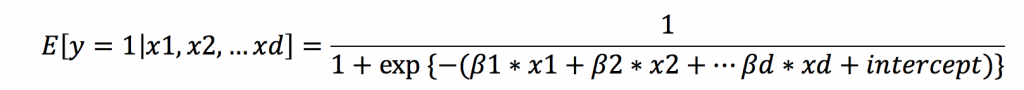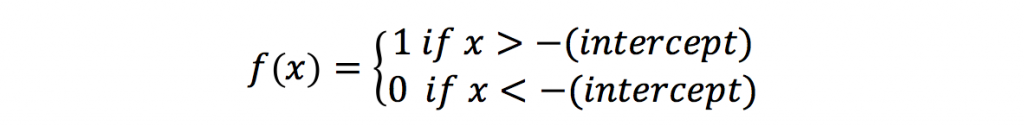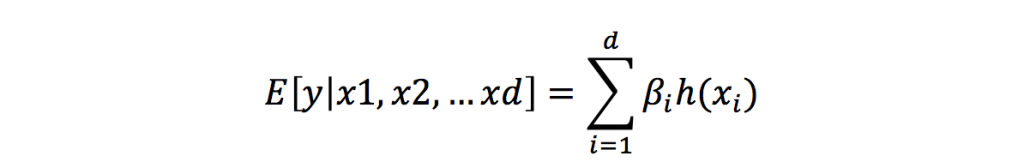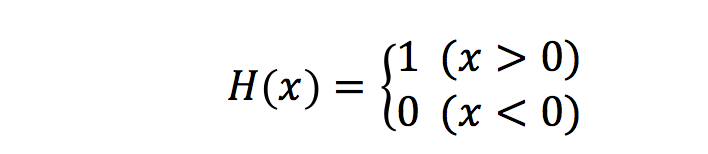こんにちは、D3の大久保です。世間は空前のニューラルネットワークブームですね。生態学もその例外ではなく、2018年3月の学会期間中はニューラルネットワークをはじめとした機械学習関連の発表が数多く見られました。こうした技術はよく「人工知能」「人間の神経細胞の挙動を模している」といった風に説明され、何やら大仰な雰囲気から「いままでの統計分析とは根本的に違うものなんだろう」と、身構えてしまう人もいるかもしれません。
しかし1ステップずつ確認していけば、本来ニューラルネットワークモデルというのは生態学者の馴染んできた統計分析と強く関連していることがわかると思います。そこで今回は、シンプルな形のニューラルネットワークモデルに焦点を絞り、このモデルが既存の非線形回帰分析の自然な拡張として理解できることを説明します。
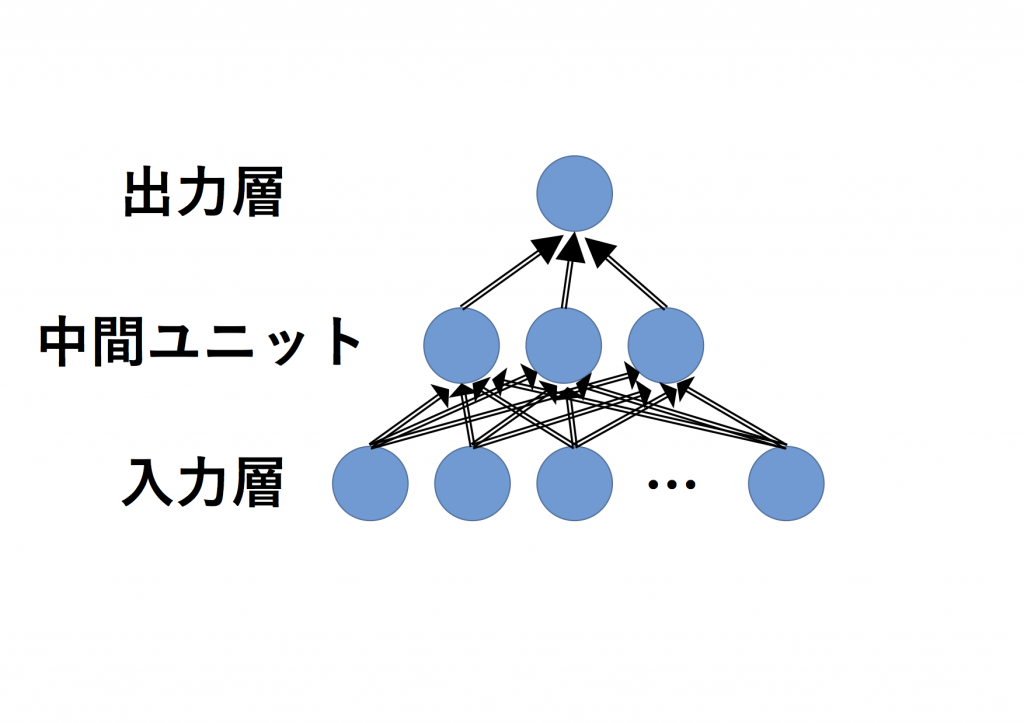
今回目指すゴールは、以下のような中間層が1層で活性化関数がシグモイド関数の場合です。近年ニューラルネットワーク研究が著しく進んでいることを考えると少し単純すぎるとも言えますが、イメージをつかむには十分に有益かと思います。
・復習
まずは、生態学研究に携わっている人なら誰でも一度は耳にしたことのある線形回帰モデル(LM)と一般化線形回帰モデル(GLM)のおさらいから始めます。目的変数をy、説明変数x1,x2,x3…xdをと置きます。まず、yが正規分布に従う場合を考えましょう。この時、に対するによる回帰モデルは以下のように表現できます。
ただし、
ここでμの値は、説明変数が与えられた時のyの期待値であることに注意しましょう。すなわち、
(E[y|・]は、「・で条件づけられたyの期待値」を意味する記号で、interceptは切片のことです。)
続いて、yが二項分布の場合を考えてみましょう。目的変数yが二項分布に従う場合によく使われるロジスティック回帰は、以下のように表現できます。
変形して以下のシグモイド関数と呼ばれる形で書くこともあります。
(E[y=1|・]は、「・で条件づけられたy=1になる確率」を意味する記号です。)
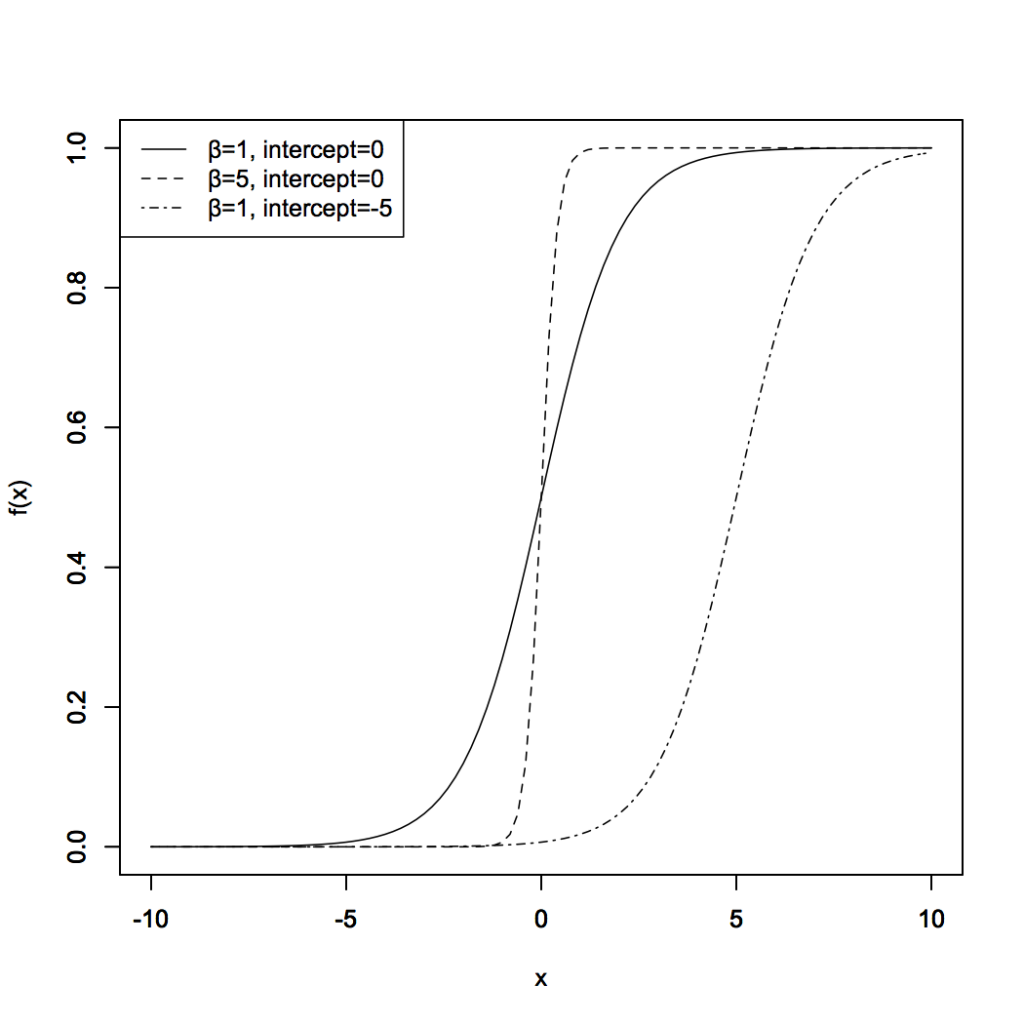
変形後の形の関数について、もう少し詳しく見ておきましょう。ここでは簡単のため、説明変数が1次元の場合だけを考え
interceptの値が小さくなると関数全体が右側にずれることが確認できます。またβの値が大きくなるほど、関数の立ち上がりが急峻になり、β=∞にちかい時には-(intercept)の値を境にして
とよく似た特性を持つだろう、とわかります。(*注 正確には、x=-(intercept)で連続か不連続かという違いもあります。)
・回帰式の基底展開
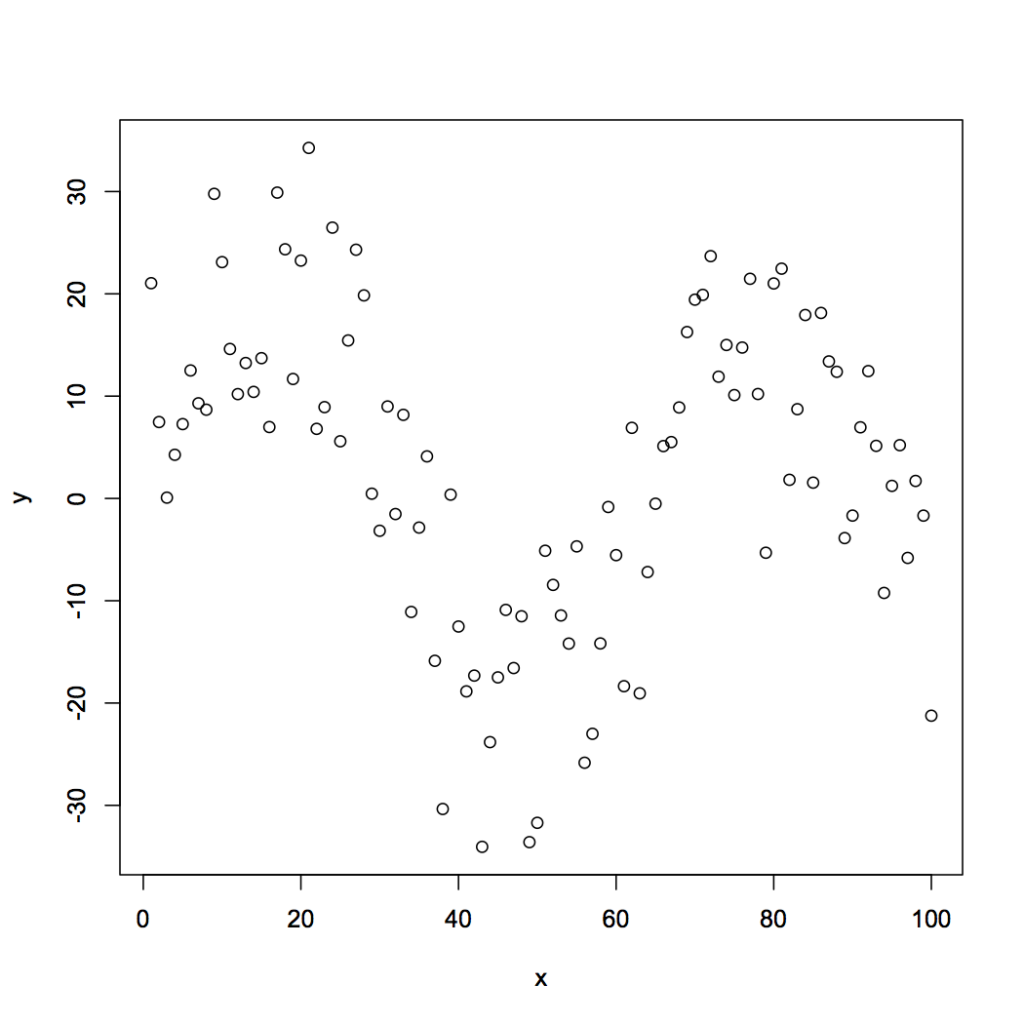
ところが、実際のデータ分析では単純な線形回帰や一般か線形回帰だけでは対応できない場合があります。例えば説明変数が1次元の場合について、以下の散布図を見てみましょう。
という形からも分かる通り、説明変数とyの間の関係性が線形であることを前提としたモデルです。散布図のように線形な回帰線では不適当な場合、どのように分析すればよいでしょうか。
ここで、新しく基底関数という概念を導入して回帰式の柔軟性を高めてみましょう。まず、これまで扱ってきたE[y|説明変数]の表記を、総和を表す記号Σで以下の形で書き直します。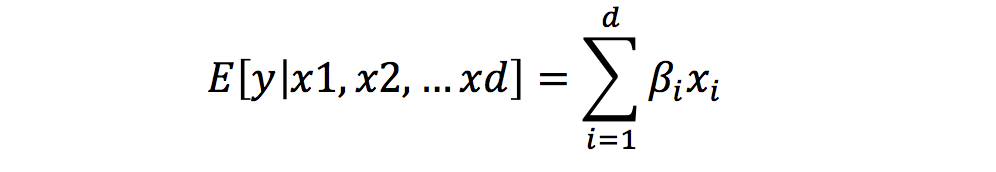
これを、以下のように一般化してみます。
ここで、h()が新たに導入された基底関数です。この表記に基づいて今までの線形回帰モデルや一般化線形回帰モデルを再解釈すると、「すべてのxについて、h(x)=x」という特別な基底関数を仮定していた、と言うことができます。説明変数と目的変数の間に線形性が成り立たない場合も考えたいのであれば、データに対して適切な基底関数h()を設定すれば良いわけです。
基底関数の中でも素朴なアイデアのひとつが、区分多項式による表現です。区分多項式とは、関数f(x)について、xの値に応じて関数をいくつか節点で切断し、節点と節点の間をそれぞれ多項式で結ぶ関数です。例えば節点が2つの場合を考えると、一般に区分多項式による基底関数は以下の形で表現できます。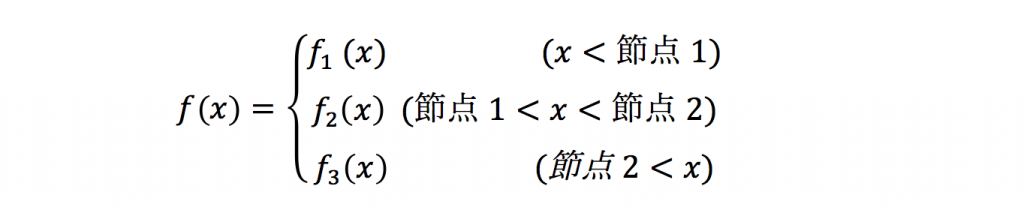
ここで、fi(x)(i=1,2,3)は、それぞれxに関する多項式です。実用的には、節点と節点を結ぶ多項式に3次式を使うことが多いのですが、ここではニューラルネットワークを説明するために0次関数を採用します。つまり以下のように、節点において不連続に変化し、節点と節点の間では定数になる関数です(a,b,cはそれぞれ定数)。
しかし、このアイデアにはまだ以下の問題が残されます。
・節点の位置をどのように決めるか
・節点と節点の間を不連続につないで良いのか
この問題に対処するにはいくつかの方法が考えられます。例えば、生態学でも以前から使われているスプラインと呼ばれる方法で解決することもできます。しかしここでは、H(x)の場合分けを実現する方法に着目してみます。
上式のような場合分けを数学的に表現するための方法に、以下の「ヘヴィサイドのステップ関数」を利用するアプローチあります。
ヘヴィサイドのステップ関数は、あたかもxの値に応じてスイッチのオン・オフを切り替えるかのような機能を持たせることができます。即ち、この関数を使って上の(1)式を書き直すと以下のようになるのです。
ここで(b-a)と{(b-a)-c}は、それぞれxが節点1と2を超えたときにf(x)がどれだけ変化するかを表していて、xが節点を超えるとステップ関数の働きでその項が“オン”になるわけです。
ところでステップ関数は、一般化線形回帰の項で確認したシグモイド関数においてβが非常に大きい場合とよく似た形をしていることを思い出しましょう。区分多項式の場合分けを二値的なオン・オフで表現していたステップ関数に替えて、なだらかな形状を持つシグモイド関数を採用すれば節点と節点の間を滑らかに繋ぐことができるのではないでしょうか。これこそが、中間層が1層のニューラルネットワークモデルなのです。つまり、中間層が1層で中間ユニットがn個のニューラルネットワークモデルは、n個の領域に切断された0次関数を滑らかに接合したものであり、各ユニットの活性化を司るシグモイド関数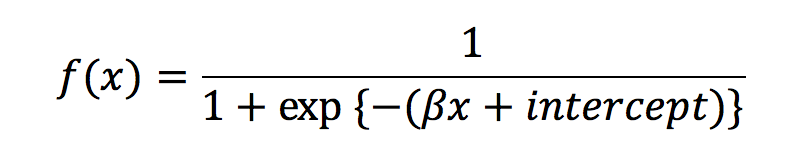
のパラメータは
β:節点と節点の接合部における滑らかさ
intercept:節点の位置
というわけです。このようにして、yに関するxの回帰線を滑らかにしつつ、データから節点の位置も自動的に推定できるのがニューラルネットワークの大きな強みです。
次回の記事では、シミュレーションで生成したデータを使ってニューラルネットワークモデルの挙動を確認します。(もしStanやWinBUGSのようなモンテカルロサンプラーがあれば、40行弱の比較的コンパクトなコードで実装できますよ!)